Seam Carving in Pure Java
Today I tried to implement seam carving in pure Java, without dependencies.
In a few words, it’s a method to automatically reduce the size of an image keeping as much details as possible. How is this accomplished? It’s done by calculating the importance of each pixel with some metric (for example, the gradient magnitude) and removing the less important pixels at first.
The result is made clear by this example from Wikipedia:
The original image, before resizing. It’s the Broadway Tower, Cotswolds, UK (thanks, Wikipedia)
The same image after resizing.


The person and the castle remained untouched, while the sky and the grass in between has been removed. GIMP has a plugin to do so, some time ago I played with it and had the idea to implement it in pure Java, as a small library.
Here it is, with some usage documentation. It’s single class, with some static methods to change the width of an image.
First, we define a metric to assign each pixel an importance level. A possible criteria is the sum of the differences between the color of the pixel and the surrounding ones. Pixels on the edge of a part of the image, like the castle or the person, have a least one neighbor with a different color, obtained as the difference of red, green and blue channel values. If the two pixels are expressed as RGB integers this value is calculated as:
Math.sqrt(Math.pow((a & 0xFF) – (b & 0xFF),2)
+ Math.pow(((a & 0xFF00) >> 8) – ((b & 0xFF00) >> 8),2)
+ Math.pow(((a & 0xFF0000) >> 16) – ((b & 0xFF0000) >> 16),2))
this value is to number between 0 (same color) and 443 (difference between black and white, since sqrt(3*256^2)=443)
Once we calculate the importance of each pixel, we cannot just remove the N pixel with the lower importance in the row, or we may remove pixels in different areas and get a shifted image like this:
The Milan skyline applying 'stupid' resizing

when we remove a pixel from a row, the others get shifted, and when we delete pixels from different areas the rows are no more aligned and we get this effect; of course the more pixels we remove the worst the image becomes.
To avoid this, we have to remove pixels along a path, so if we remove the one at (x,y) we’ll then proceed to remove the one at (x,y+1) or (x+1,y+1) or (x-1,y+1), not just anyone in the row, preserving the shapes of the image.
To find the path through the image with the lower importance I used this algorithm:
- Create a matrix with the same size of the image, we’ll call this matrix minimum cumulative importance, MCI.
- Set the bottom row of MCI to 0
- For each remaining row from the bottom to the top, calculate the MCI value as the sum of the importance of the corresponding pixel an the minimum importance among the three underlying pixels
- Now find the lowest value in the top row, let’s call its column number xl (X coordinate of the Less important), and mark it
- At the second row from the top, find the lowest MCI value among the three on column xl-1, xl and xl+1, mark it
- Continue iterating over the rows, marking one pixel for each one, always picking among the three pixels right under the one chosen at the previous row
This is the same method used by hidden Markov models to calculate the hidden state sequence, called forward–backward algorithm.
Now, what to do if we want to remove more than one pixel? We can calculate the MCI matrix once and find the shortest paths many times, marking the already found ones and avoiding them when choosing the pixels in the steps 4 and 5.
This doesn’t work: we can have many paths creating Y-shaped pattern which at some point doesn’t leave pixels free for new paths. In this case, we can allow the exception and let the path skip to the less important pixel in that row not marked by other paths, risking the same effect we got on stupid resizing above.
The result is this:

The image resized removing 300 paths, allowing paths to “jump” when other paths took all the available pixels
Better than before, but still awful. The paths tends to be close to each others, as we can see drawing them:

The paths to remove from the picture, marked in negative. Do you see the paths appearing from the center of the image? Those have “jumped” and are causing that awful effect
This is the MCI matrix, red pixels are the most important
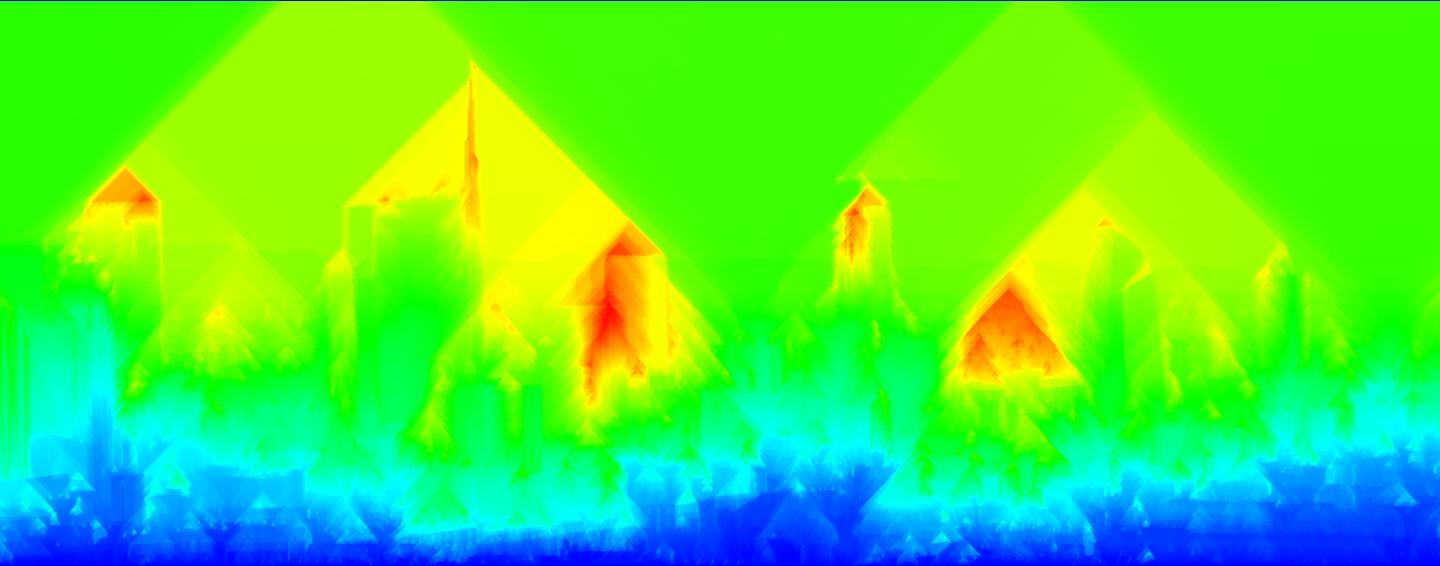
The minimum cumulative importance matrix of the Milan skyline picture. The color of a pixel represent the minimum cumulative cost (importance) of the path to reach it from the bottom.
You can note that the triangular “stains” left by the high variance parts: the edges of those triangles are the paths able to bypass them, following a 45° direction.
The solution is to remove one path and recalculate the MCI many times. As you may guess, this is painfully slow, but the result is way better:

The Milan skyline resized by recalculating the MCI matrix after each path removal
Images full of straight lines are harder to resize, let’s try with my favorite painter, Hieronymus Bosch, and his most famous paint, The Garden of Earthly Delights:

The Garden of Earthly Delights – original
This is the MCI matrix:
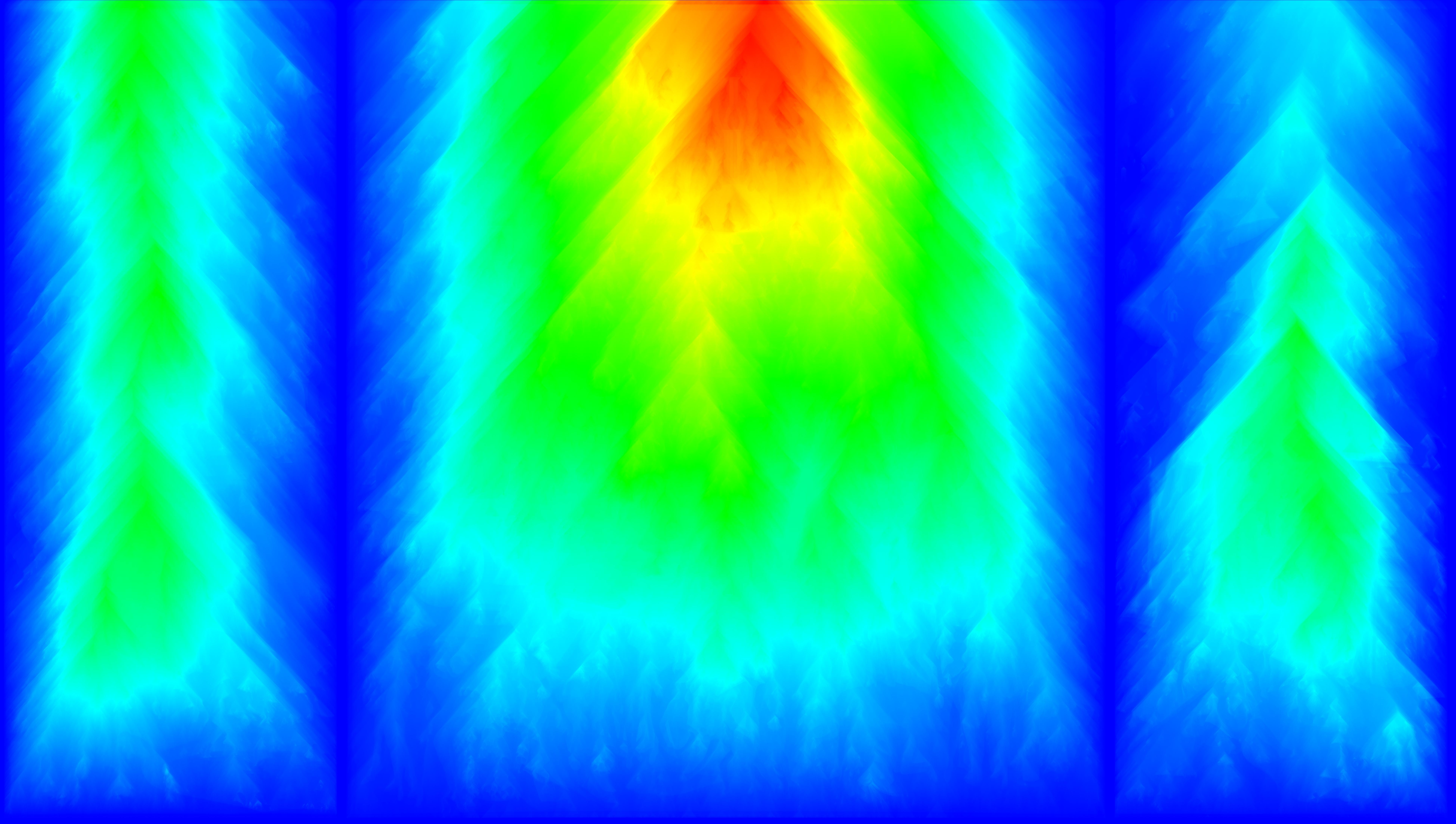
The Garden of Earthly Delights – pixel importance
Unsurprisingly, the borders between the panels are the less important area. And in fact, they get removed

The Garden of Earthly Delights – pixel importance
And here the same example with a street

The original street picture

The resized street picture

Pixel values of the street picture